Halo Sahabat, berikut ini adalah Soal dan Pembahasan Matematika Dasar Eksponen atau bilangan berpangkat. Eksponen atau Bilangan berpangkat adalah salah satu operasi aljabar setelah kita belajar Perkalian dan penjumlahan. Salah satu fungsi paling sederhana dari bilangan berpangkat ini adalah menyederhanakan penulisan bilangan yang sangat besar atau bilangan yang sangat kecil.
Dari fungsi bilangan berpangkat yang sangat sederhana tetapi sangat bermanfaat sehingga sangat banyak modifikasi bentuk soal tentang eksponen ini. Tetapi mempelajari dan menggunakan aturan-aturan pada eksponen juga sangatlah mudah, jika Sahabat mengikuti step by step yang kita diskusikan dibawah ini, maka Sahabat akan dengan mudah memahami soal-soal eksponen dan menemukan solusinya.
12&space;\\(B)15&space;\\(C)18&space;\\(D)21&space;\\(E)24)
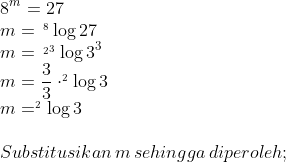
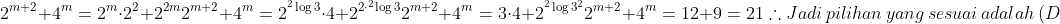21)
Dari fungsi bilangan berpangkat yang sangat sederhana tetapi sangat bermanfaat sehingga sangat banyak modifikasi bentuk soal tentang eksponen ini. Tetapi mempelajari dan menggunakan aturan-aturan pada eksponen juga sangatlah mudah, jika Sahabat mengikuti step by step yang kita diskusikan dibawah ini, maka Sahabat akan dengan mudah memahami soal-soal eksponen dan menemukan solusinya.
Pada dasarnya antara Eksponen atau Bilangan Berpangkat, Bentuk Akar, dan Logaritma mempunyai keterkaitan sangat erat.
Kesulitan menganalisa kalimat soal mungkin bisa jadi salah satu masalah dalam diskusi tentang eksponen yang umumnya dilakukan di kelas.
Seperti apa tingkat kesulitan soal tentang Matematika Dasar Eksponen , mari kita simak beberapa sampel soal untuk kita diskusikan yang kita ambi dari soal-soal SBMPTN (Seleksi Bersama Masuk Perguruan Tinggi Negeri) atau SMMPTN (Seleksi Mandiri Masuk Perguruan Tinggi Negeri) dan UN (Ujian Nasional) atau dari soal-soal simulasi di sekolah.
Sebagai catatan, beberapa aturan dasar sederhana pada Eksponen berikut ini mungkin membantu dalam menyelesaikan masalah yang berkaitan dengan eksponen atau bilangan berpangkat;
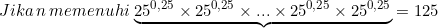
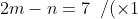&space;\\\frac{m+6n=10\,&space;\,&space;/(\times&space;2)}{2m-n=7\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,}&space;\\\frac{2m+12n=20\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;-\,&space;\,&space;\,&space;\,&space;\,}{-13n=-13}&space;\\Sehingga&space;\,\mathbf{n}=1)
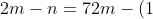=7&space;\\2m=7+1&space;\\2m=8&space;\\m=4)
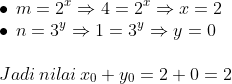
2)
![\\Nilai\, x\, yang\, memenuhi\,persamaan\,3^{2x+3}=\sqrt[3]{27^{x+5}}\,adalah... \\(A)-2 \\(B)-1 \\(C)0 \\(D)1 \\(E)2](https://latex.codecogs.com/gif.latex?\\Nilai\,&space;x\,&space;yang\,&space;memenuhi\,persamaan\,3^{2x+3}=\sqrt[3]{27^{x+5}}\,adalah...&space;\\(A)-2&space;\\(B)-1&space;\\(C)0&space;\\(D)1&space;\\(E)2)
![\\3^{2x+3}=\sqrt[3]{27^{x+5}} \\3^{2x+3}=27^{\frac{x+5}{3}} \\3^{2x+3}=(3^{3})^{\frac{x+5}{3}} \\3^{2x+3}=3^{x+5} \\ \\\Rightarrow 2x+3=x+5 \\\Rightarrow 2x-x=5-3 \\\Rightarrow \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, x=2 \\ \\\therefore Pilihan\, yang\, sesuai\,adalah\,(E)2](https://latex.codecogs.com/gif.latex?\\3^{2x+3}=\sqrt[3]{27^{x+5}}&space;\\3^{2x+3}=27^{\frac{x+5}{3}}&space;\\3^{2x+3}=(3^{3})^{\frac{x+5}{3}}&space;\\3^{2x+3}=3^{x+5}&space;\\&space;\\\Rightarrow&space;2x+3=x+5&space;\\\Rightarrow&space;2x-x=5-3&space;\\\Rightarrow&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;\,&space;x=2&space;\\&space;\\\therefore&space;Pilihan\,&space;yang\,&space;sesuai\,adalah\,(E)2)
29&space;\\(B)28&space;\\(C)27&space;\\(D)26&space;\\(E)25)
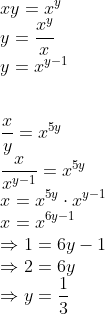
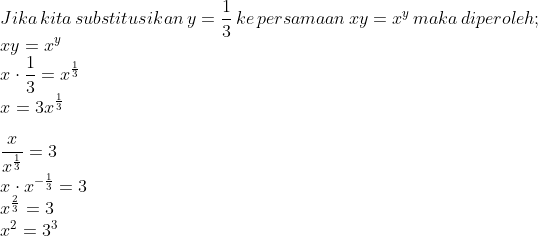
28)
}{g(x)}=\frac{2^{2x}+2^{x+1}-3}{2^{x}+3}&space;\\\frac{f(x)}{g(x)}=\frac{(2^{x})^{2}+2^{x}\cdot&space;2-3}{2^{x}+3}&space;\\&space;\\Untuk\,mempermudah\,kita\,dapat\,memisalkan\,2^{x}=m&space;\\sehingga\,diperoleh;&space;\\\\\frac{f(x)}{g(x)}=\frac{(m)^{2}+m\cdot&space;2-3}{m+3}&space;\\\\\frac{f(x)}{g(x)}=\frac{(m)^{2}+2m-3}{m+3}&space;\\\\\frac{f(x)}{g(x)}=\frac{(m+3)(m-1)}{m+3}&space;\\\\\frac{f(x)}{g(x)}=m-1&space;\\Jadi\,\frac{f(x)}{g(x)}=2^{x}-1&space;\\&space;\\\therefore&space;Pilihan\,yang\,sesuai\,adalah\,(D)2^{x}-1)
Kesulitan menganalisa kalimat soal mungkin bisa jadi salah satu masalah dalam diskusi tentang eksponen yang umumnya dilakukan di kelas.
Seperti apa tingkat kesulitan soal tentang Matematika Dasar Eksponen , mari kita simak beberapa sampel soal untuk kita diskusikan yang kita ambi dari soal-soal SBMPTN (Seleksi Bersama Masuk Perguruan Tinggi Negeri) atau SMMPTN (Seleksi Mandiri Masuk Perguruan Tinggi Negeri) dan UN (Ujian Nasional) atau dari soal-soal simulasi di sekolah.
Sebagai catatan, beberapa aturan dasar sederhana pada Eksponen berikut ini mungkin membantu dalam menyelesaikan masalah yang berkaitan dengan eksponen atau bilangan berpangkat;
No 1. Soal SNMPTN 2010 Kode 336
No 3. Soal SPMB 2003 [Regional I]
Alternatif Pembahasan :
No 4. Soal SIMAK UI 2012 Kode 221
Alternatif Pembahasan :
No 5. Soal SPMB 2005 Kode 470
Alternatif Pembahasan :
No 6. Soal SBMPTN 2013 Kode 327
Alternatif Pembahasan :












